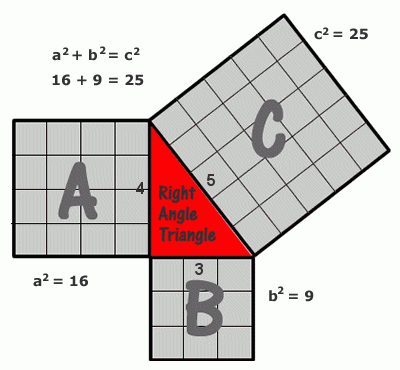
Pythagorova věta
Pythagorova věta popisuje vztah, který platí mezi délkami stran v pravoúhlém trojúhelníku v rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníka, pokud jsou známy délky dvou zbývajících stran.
Pythagorova věta zní:
V pravoúhlém trojúhelníku platí, že obsah čtverce sestrojeného nad přeponou je roven součtu obsahů čtverců sestrojených nad oběma odvěsnami.
Přepona je nejdelší strana a odvěsna jsou dvě kratší strany v pravoúhlém trojúhelníku.

Formálně Pythagorovu větu vyjadřuje rovnice:
a2 + b2 = c2
kde
písmeno c označuje délku přepony,
písmena a a b označují délky odvěsen pravoúhlého trojúhelníku.
Rovnice pro výpočet délky přepony:
c2 = a2 + b2
Rovnice pro výpočet délek odvěsen:
a2 = c2 - b2
b2 = c2 - a2
Pythagorovu větu lze použít i obráceně ke zjištění, zda je daný trojúhelník pravoúhlý.
Obrácená Pythagorova věta zní:
Jestliže v trojúhelníku platí, že součet obsahů čtverců sestrojených nad kratšími stranami je roven obsahu čtverce sestrojeného nad nejdelší stranou, potom je tento trojúhelník pravoúhlý.
Pythagorejský trojúhelník
Pythagorejský trojúhelník je pravoúhlý trojúhelník, jehož délky strany jsou vyjádřeny celými (přirozenými) čísly.
Nejznámnější pythagorejský trojúhelník má délky stran 3, 4, 5.
Pro délky stran v pravoúhlém trojúhelníku platí Pythagorova věta (viz výše), proto musí pro trojici čísel 3, 4, 5 platit 32 + 42 = 52
Jiné trojice přirozených čísel, které jsou délkami stran pythagorejských trojúhelníků jsou např.:
6, 8, 10; 8, 15, 17; 5, 12, 13; 12, 16, 20; 20, 21, 29; apod.
Těmto trojicím přirozených čísel říkáme Pythagorejská čísla.